Imaginemos que tenemos una tabla con la altitud de las cien mil ciudades más pobladas del mundo y consideramos el primer dígito que indica su altitud. Por ejemplo, a Madrid (657 metros) la asociaríamos con el dígito 6, a México DF (2850 metros) con el 2, a Nueva York (10 metros) con el 1, etc…
Con tantos ítems puede presuponerse que ese primer dígito puede distribuirse uniformemente entre todas las posibilidades de 1 a 9 y que los dígitos aparecen razonablemente un 11,11 % (100/9) cada uno aproximadamente.
No es así. En realidad, la frecuencia con que aparece el dígito 1 es mayor que la frecuencia con que aparece el 2, y ésta mayor que la que aparece el 3… y, así, sucesivamente.
En la imagen aparece, en la parte superior, la hipotética distribución de frecuencias y, debajo, la real:
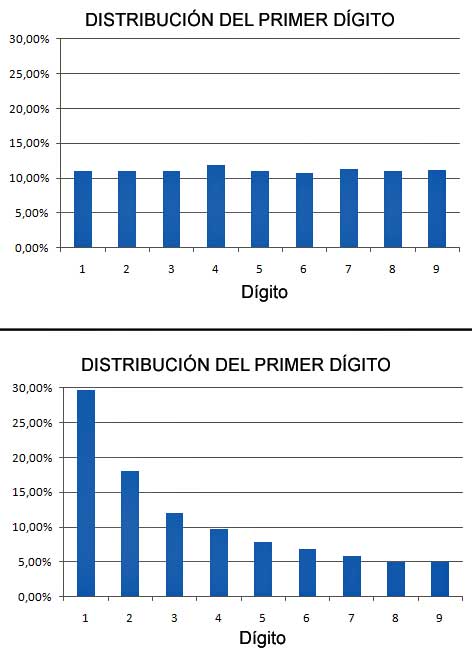
El número de veces para las que el primer dígito es un 1 es de casi el 30 % y es un 9 menos del 5% de las veces.
Y lo curioso es que esto sucede prácticamente SIEMPRE. Y cuando digo siempre me refiero a que no importa el origen de los datos numéricos: si éstos son homogéneos y producto de una recopilación de valores sobre variados aspectos y contextos de la vida real (y lo suficientemente abundantes) sus primeros dígitos mantienen una distribución similar como es el caso de series de precios de acciones, número de habitantes, tasas de mortalidad, longitud de los ríos, números primos, etc.
Este hecho se conoce como la Ley de Newcomb–Benford debido a los dos primeros científicos que la consideraron.
La fórmula de Benford indica que la probabilidad de ser n el primer dígito de un cierto valor es descrita por la siguiente expresión:

Y más: esta fórmula vale para calcular la probabilidad de que un número n cualquiera coincida con los primeros dígitos de los valores del estudio que hagamos.
Una aplicación de esta ley se encuentra en la detección de fraudes. La mayoría de las personas que cometen fraude con los números no son conscientes de la Ley de Benford; tablas de declaraciones de impuestos, informes de gastos, registros de ventas deben seguir, todos los datos, una distribución de Benford.

Eso quiere decir que en la muestras con el numeral 1 serían más consideradas, en lugar de las del 9, a manera de ejemplo en una revisión de una muestra, no veo la importancia del tema para el asunto del fraude o la corrupción a que alude el aporte. Saludos,
Me gustaMe gusta
La ley de Benford aplica para determinar tanto errores como fraudes. A nivel de errores podríamos mencionar el tema de duplicaciones de información (registro de dos o más transacciones en forma incorrecta o sin dolo por ejemplo pagos duplicados uno con cheque y otro con transferencia) o fraude (fragmentación de compras para no ser detectados con un límite de transacción). Al encontrar un número que excede principalmente el número máximo, según la población específica y según la formula indicada, se convierte en sospechoso y ahí empezaría la investigación.
Una consideración importante es que la Ley de Benford considera los números de izquierda a derecha, por ejemplo 0,01 – 1 – 100 – 1000 – 1.000.000 todos quedarían en la «familia» del número 1. Teniendo esta población un ordenamiento de datos en forma inversa detectaría los que podrían tener mayor impacto en una familia y por ende mayor revisión.
Otro punto es que los dígitos se cuentan de izquierda a derecha pero se tiene una «profundidad» en el análisis esto es la cantidad de dígitos a analizar, entre más dígitos se usen más exacto es el ejercicio para detectar los posibles errores o fraudes.
Adicionalmente un ejercicio importante es tener en cuenta que una vez detectado un caso sospechoso se podría filtrar la información del cliente o entidad para revisar si fue un hecho esporádico o si fue en realidad un evento fraudulento. Normalmente el modus operandi de un criminal inconscientemente genera un rango de número similares siempre.
El Software ACL es una herramienta que permite hacer este y otros tipos de ejercicios y cálculos para determinar este posible tipo de problemas en los datos bajo análisis.
Me gustaMe gusta
Es interesante el artículo pues generalmente quien comete Fraude quiere recrear un ambiente de normalidad en algo que en este caso no es y lo paradójico es que precisamente la existencia de esta normalidad es un potencial indicador de algo anormal. Muy buen artículo
Me gustaMe gusta
Gracias Javier por tus reflexiones…. un saludo
Me gustaMe gusta